最优化算法总结 (最优化算法总结报告)

本文目录导航：

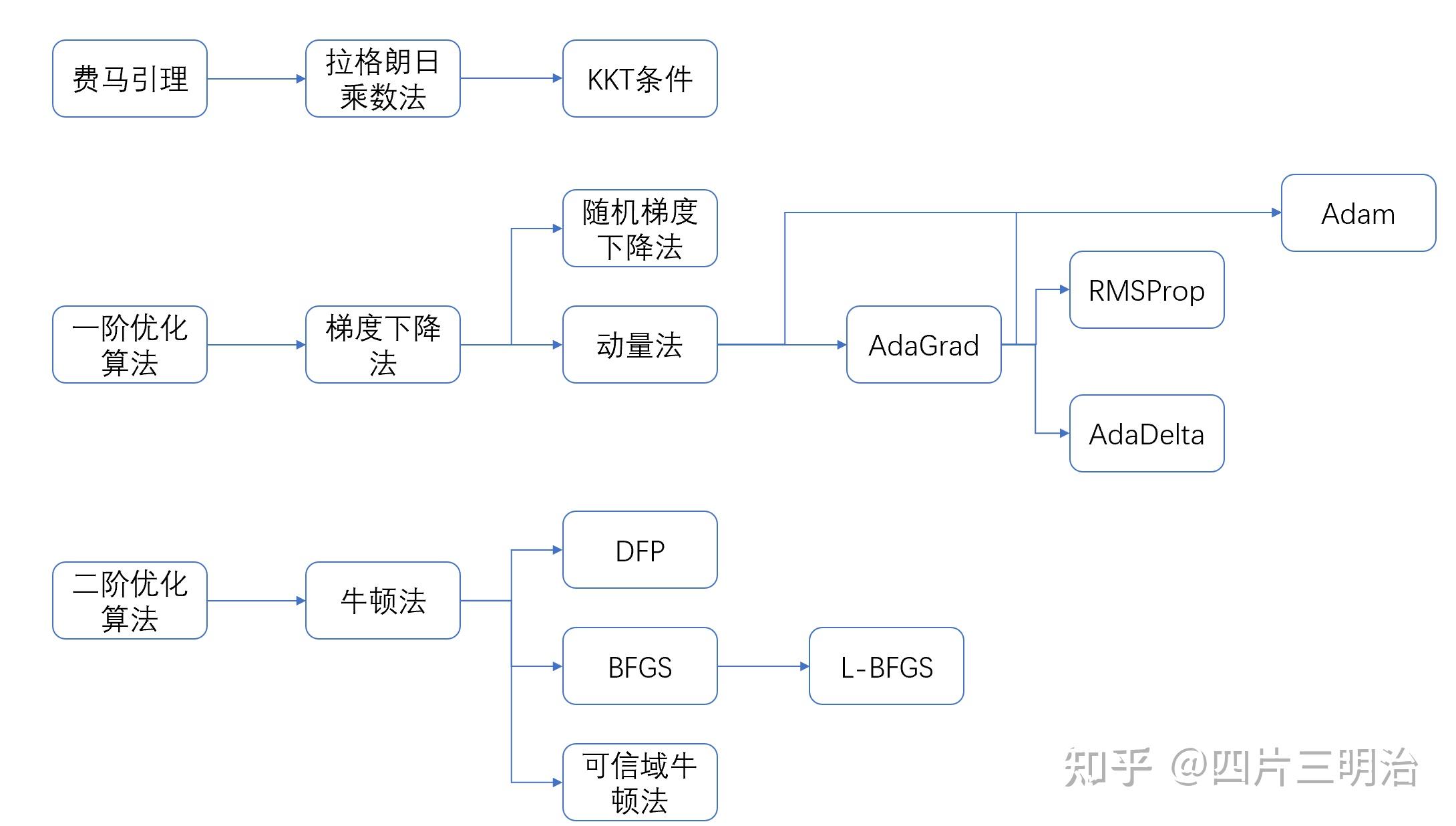
• 最优化算法总结
• 探求最优化算法的艺术：寻觅函数极值的迷信之路
• 深度学习中的优化器学习总结
• 非线性优化方法的总结——approximation

最优化算法总结

探求最优化算法的艺术：寻觅函数极值的迷信之路

机器学习的外围应战在于经过求解指标函数的极值来驱动模型的提高，这个环节理论转化为寻觅最小值。

微积分中的导数是寻觅极值的利器，但在实践疑问中，咱们往往面临非润滑的函数。

在多元函数的环球里，梯度作为导数的向量裁减，起着关键作用，极值点要求梯度为零。

但是，判别极值类型并非易事，Hessian矩阵（二阶导数矩阵）为咱们提醒了答案：

数值优化算法，如梯度降低、一阶或二阶优化，为咱们提供了探求的工具。

在遇到逾越方程这类复杂疑问时，它们经过迭代，应用导数消息逐渐迫近极值。

一阶优化如梯度降低，经过一元函数的泰勒倒退，调整方向，确保函数值降低。

多元状况下，选用适合的方向至关关键，比如梯度降低法，它的迭代环节如下：

变种的梯度降低方法如动量梯度降低（参与动量项），自顺应算法如AdaGrad和AdaDelta（区分依据历史梯度调整学习率和处置学习率过快衰减疑问）进一步优化功能。以下是部分方法的简明概述：

相较于梯度降低，二阶优化算法如牛顿法虽更准确，但代价是计算Hessian矩阵的复杂度和存储需求。

在小批量处置中，二阶导数的预计误差较大，或许造成模型不稳固。

总的来说，最优化算法是一场精细的舞蹈，每一步都须要精准计算和奇妙设计。

经过了解这些外围原理和算法，咱们能在机器学习的陆地中找到最优解的航标。

想了解更多，无妨深化探求这个神奇的畛域，链接在这里就不再赘述了。

深度学习中的优化器学习总结

梯度降低法1.批梯度降低法（Batch Gradient Descent）一次性迭代训练一切样本，样本总数为n, 学习训练的模型参数为W，代价函数为J(W)，输入和输入的样本区分为X^i,Y^i, 则代价函数关于模型参数的偏导数即关系梯度为ΔJ(W)，学习率为η_t好处：现实形态下经过足够多的迭代后可以到达全局最优；缺陷：关于大数据集，训练速度会很慢2.随机梯度降低法（Stochastic Gradient Descent）为了放慢收敛速度，每次训练的都是随机的一个样本；好处：训练速度快，引入了噪声（随机选取样本），使得或许会防止堕入部分最优解；-Batch Gradient DescentBGD 和 SGD的折中打算， batch_size = 1， 就是 SGD， batch_size = m 就是Mini-Batch Gradient Descent,（如今深度学习中很多间接把Mini-Batch Gradient Descent 简称为SGD, 提到SGD 普通指的就是Mini-Batch Gradient Descent；好处：mini-batch gradient descent 相对SGD在降低的时刻，相对平滑些（相对稳固），不像SGD那样震荡的比拟凶猛。

缺陷：参与了一个超参数 batch_size，要去调这个超参数；动量优化法从训练集中取一个大小为n的小批量{X^1,X^2,...,X^n}样本，对应的实在值区分为Y^i，则Momentum优化表白式为其中v_t示意 t 时辰积聚的减速度，α示意能源的大小，普通取值为0.9；动量关键处置SGD的两个疑问：一是随机梯度的方法（引入的噪声）；二是Hessian矩阵病态疑问（不是很了解）。

了解战略为：因为以后权值的扭转会遭到上一次性权值扭转的影响，相似于小球向下滚动的时刻带上了惯性。

这样可以放慢小球向下滚动的速度。

2.牛顿减速度梯度法（Nesterov Accelerated Gradient）了解战略：在Momentun中小球会自觉地跟从下坡的梯度，容易出现失误。

所以须要一个更痴呆的小球，能提早知道它要去哪里，还要知道走到坡底的时刻速度慢上去而不是又冲上另一个坡。

计算W_t−αv_{t−1}可以示意小球下一个位置大略在哪里。

从而可以提早知道下一个位置的梯度，而后经常使用到以后位置来降级参数。

自顺应学习率优化算法算法假设一个多分类疑问，i示意第i个分类，t示意第t迭代同时也示意分类i累计出现的次数。

η_0示意初始的学习率取值普通为0.01，ϵ是一个取值很小的数（普通为1e-8）为了防止分母为0。

W_t示意t时辰即第t迭代模型的参数，g_{t,i}=ΔJ(W_{t,i})示意t时辰，指定分类i，代价函数J(⋅)关于W的梯度。

从表白式可以看出，对出现比拟多的类别数据，Adagrad给予越来越小的学习率，而关于比拟少的类别数据，会给予较大的学习率。

因此Adagrad适用于数据稠密或许散布不平衡的数据集。

Adagrad 的关键好处在于不须要人为的调理学习率，它可以智能调理；缺陷在于，随着迭代次数增多，学习率会越来越小，最终会趋近于0。

算法RMSProp算法修正了AdaGrad的梯度积聚为指数加权的移动平均，使得其在非凸设定下成果更好其中，W_t示意t时辰即第t迭代模型的参数，g_t=ΔJ(W_t)示意t次迭代代价函数关于W的梯度大小，E[g^2]t示意前t次的梯度平方的均值。

α示意能源（理论设置为0.9），η0示意全局初始学习率。

ϵ是一个取值很小的数（普通为1e-8）为了防止分母为0。

RMSProp自创了Adagrad的思维，观察表白式，分母为sqrt(E[g^2]_t+ϵ)。

因为取了个加权平均，防止了学习率越来越低的疑问，而且能自顺应地调理学习率。

RMSProp算法在阅历上曾经被证实是一种有效且适用的深度神经网络优化算法。

目前它是深度学习从业者经常驳回的优化方法之一。

3. AdaDelta算法AdaGrad算法和RMSProp算法都须要指定全局学习率，AdaDelta算法联合两种算法每次参数的降级步长即：AdaDelta不须要设置一个自动的全局学习率好处：在模型训练的初期和中期，AdaDelta体现很好，减速成果不错，训练速度快。

缺陷：在模型训练的前期，模型会重复地在部分最小值左近颤抖。

4. Adam算法Adam中动量间接并入了梯度一阶矩（指数加权）的预计，Adam包括偏置修正，修正从原点初始化的一阶矩（动量项）和（非中心的）二阶矩预计其中，m_t和v_t区分为一阶动量项和二阶动量项。

β_1,β_2为能源值大小理论区分取0.9和0.999；m^t,v^t区分为各自的修正值。

Adam理论被以为对超参数的选用相当鲁棒，虽然学习率有时须要从倡导的自动修正；对比① 在运转速度方面两个动量优化器Momentum和NAG的速度最快，其次是三个自顺应学习率优化器AdaGrad、AdaDelta以及RMSProp，最慢的则是SGD。

② 在收敛轨迹方面两个动量优化器虽然运转速度很快，但是初中期走了很长的”岔路”。

三个自顺应优化器中，Adagrad初期走了岔路，但起初迅速地调整了上来，但相比其余两个走的路最长；AdaDelta和RMSprop的运转轨迹差不多，但在快凑近指标的时刻，RMSProp会出现很显著的颤抖。

SGD相比于其余优化器，走的门路是最短的，路子也比拟正。

干流的观念以为：Adam等自顺应学习率算法关于稠密数据具备好处，且收敛速度很快；但精调参数的SGD（+Momentum）往往能够取得更好的最终结果

非线性优化方法的总结——approximation

我想要分享我关于优化方法的了解，从确定的到随机的，从一阶到二阶，从原始到对偶，从润滑到非润滑。

我以为迭代算法就是一个始终迫近的环节，将复杂的疑问简化成多个便捷疑问的环节。

因此，我从迫近的角度来讲述这些方法。

欢迎大家来探讨交换，因为我的才干有限，或许会有疏漏或失误，宿愿大家能指出。

一、确定方法思考疑问一、1.一阶方法最早的梯度方法，经过在迭代点启动泰勒倒退获取一个部分二次函数，而后求解该函数获取新的迭代点。

一、2.二阶方法对原函数启动二阶泰勒倒退，获取牛顿方法。

当维数太大时，经常使用向量迫近，获取拟牛顿方法。

还可以依据泰勒倒退的逼远水平来选择每一步的幅度，获取信任域方法。

二、随机方法当疑问规模很大时，可以经常使用部分梯度来迫近函数，例如随机梯度（SGD）。

还可以经过批量梯度、SVRG、SARAH等方法来缩小方差。

三、邻近类方法这类方法用于处置含有非润滑项的疑问，其邻近算子容易计算。

例如，邻近点算法（PPA）、邻近梯度算法（PGA）、邻近牛顿算法（PNA）等。

四、对偶类方法从原始、对偶、原始对偶三个角度设计算法，例如增广拉格朗日方法（ALM）、交替方向乘子法（ADMM）等。

从“approximations”的角度来看，很多优化方法都离不开泰勒倒退这个工具。